Many people consider mathematics a waste of time. I disagree.
There are so many basic mechanisms in life which go back to simple mathematical concepts, especially of statistical nature. And too many people act all surprised by the (all too foreseeable) outcomes.
Especially the concepts that are of statistical nature lend themselves to be played around with numerically. In the posts of the present category, that’s what I typically do. Doing so helps me to solidify some intuitively preconceived understandings; and the result is easy to share when such a concept comes up during a discussion.
— — —
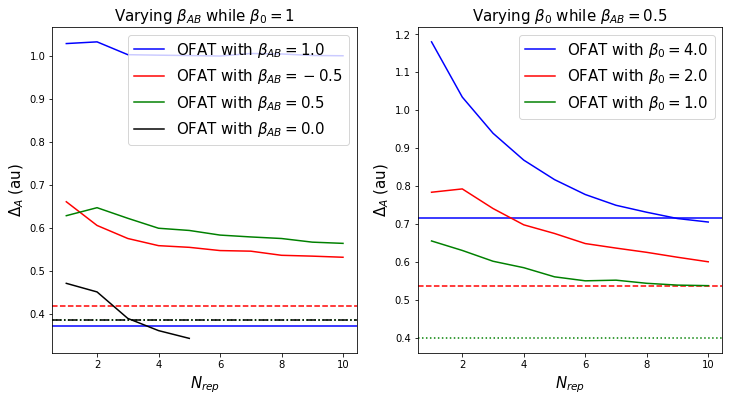
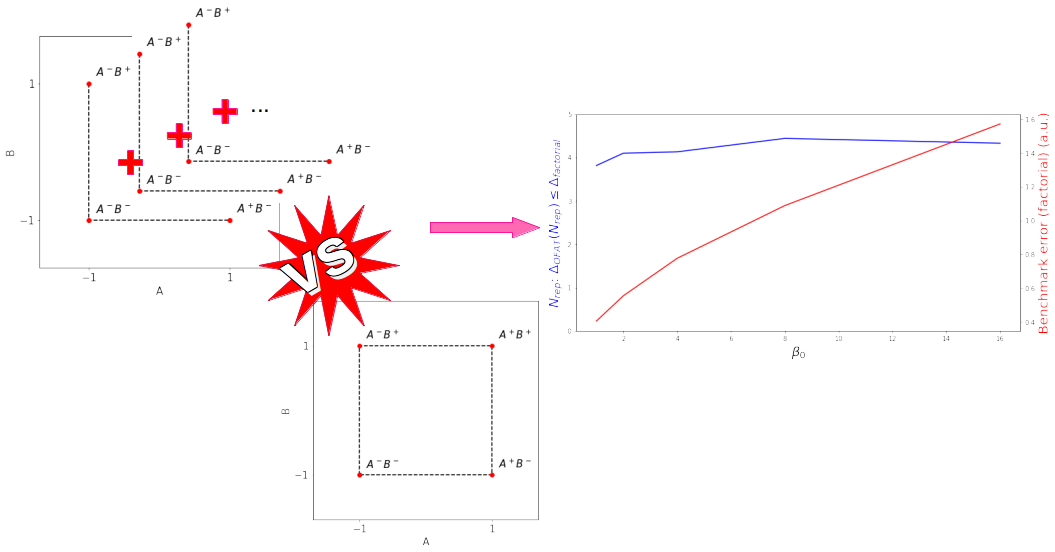
The ``one factor at a time (OFAT)'' approach isn't suited if there is an interaction factor present in a multi factor experiment. In the present post I explore the shortcomings of the OFAT versus factorial approach in more detail. In a first post about Designed Experiments, I have shown the…
From time to time I want to optimize a system, or at least explore how sensitive it is to changes. For example, I may want to optimize (i.e. reduce) the curing time of an epoxy, with the parameters being the curing temperature and the dispensing quantity or method. Or maybe…
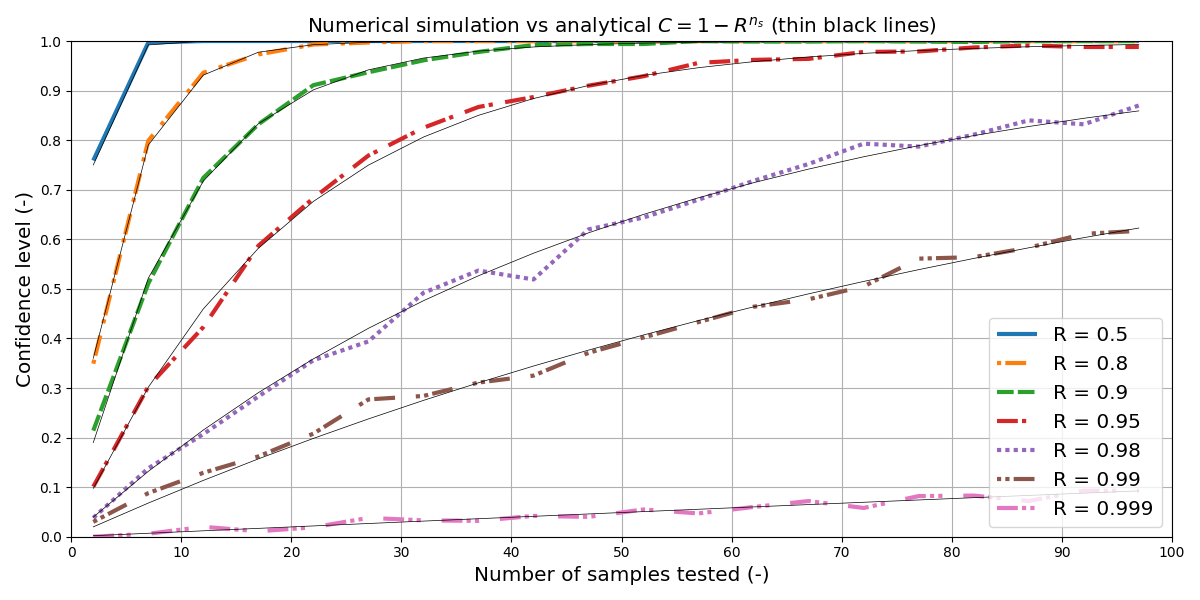
Let's say we conduct a fail/pass test. We subject $n_\mathrm{s}$ samples to an accelerated (representative) life test of $m=1$ lifetime equivalents. The test is considered a success if $100\,\%$ of the $n_\mathrm{s}$ samples survive. Yet, this leaves the important question of how certain can we be that the population as…
As discussed in another post, the signal to noise ratio (SNR) in a measurement generally improves proportional to the square root of the number of individual measurements. While I have motivated and derived the square root argument heuristically in this other post, in the present one I want to add…
The signal to noise ratio (SNR) in a measurement generally improves as one increases the acquisition time, or as one adds up over an increasing number of individual measurements, respectively. The scaling behavior is approximately proportional to the square root of the number of individual measurements. In this post I…